Razón Trigonométrica

Recuerde que una razón es una comparación entre dos cantidades o variables que se expresan como una fracción, es decir , cuando se relaciona con trigonometría las literales representan características de un triángulo rectángulo.

Una manera para definir las razones trigonométricas es exclusivamente para un triángulo rectángulo. Un triángulo rectángulo es aquel que presenta un ángulo recto en uno de sus ángulos interiores. Los lados que forma el ángulo recto se llaman catetos y el lado restante se llama hipotenusa. Al considerar un ángulo interior agudo, los nombres de los catetos cambian de nombre, ahora es cateto adyacente si forma parte del ángulo y cateto opuesto si se encuentra enfrente del ángulo considerado. Como lo muestra la figura 1 

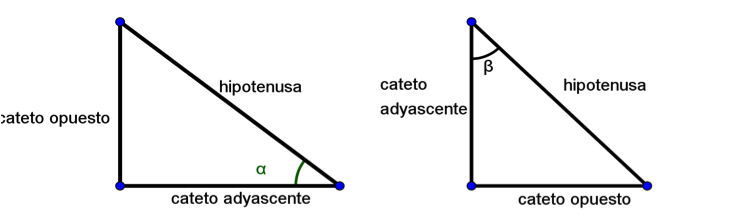
Figura 1

Al comparar los lados del triángulo rectángulo de acuerdo con la figura 1, se obtiene las siguientes razones, se les asignan un nombre y considerando el ángulo 𝞫 (beta) se obtiene:  

Generalmente los nombres se abrevian de la siguiente forma: Seno𝞫= sen 𝞫, coseno𝞫= cos 𝞫 tangente𝞫= tan𝞫, cotangente  𝞫=cot b, secante𝞫= sec 𝞫,  cosecante 𝞫= csc 𝞫. Los nombres se abrevian como cateto opuesto = c.o, cateto adyacente = c.a,e hipotenusa =h

De acuerdo a la figura 1 y las abreviaturas, las razones trigonométricas se pueden escribir como: 

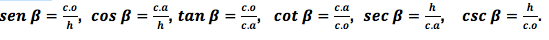
El valor numérico de las razones trigonométricas depende del ángulo y no del tamaño del triángulo rectángulo, de acuerdo con esto, se puede extender las razones trigonométricas para cualquier medida del ángulo, es decir para ángulos mayores a 90°, y no solo restringirse a ángulos agudos.