Forma simétrica de la ecuación de una recta

Este tipo de ecuación determina las distancias de los puntos de intersección de la recta al origen del sistema coordenado, como se muestra en la figura 5.

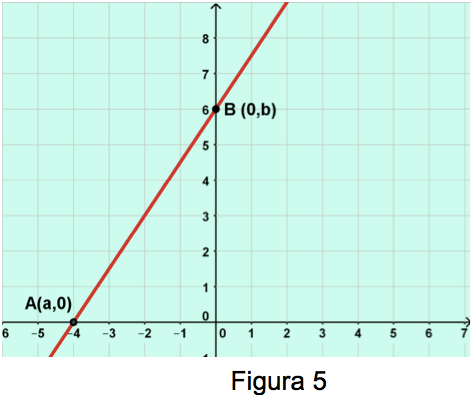
Es importante recordar que un punto está representado por un par ordenado (x, y), donde "x" recibe el nombre de abscisa, recibe el nombre de ordenada. De acuerdo a la figura 5 la ordenada al origen es "b" (distancia entre el origen y el punto de intersección de la recta con el eje "y").

La abscisa al origen es "a" (distancia entre el origen y el punto de intersección de la recta con el eje "x"). de esta forma se tienen los puntos A(a,0) y B(b,0) que son puntos de la recta que al sustituir en la ecuación de la recta en su forma punto-punto y realizar las operaciones correspondientes se obtiene la expresión.  

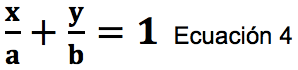
La ecuación cuatro se le llama ecuación simétrica de la recta y la empleamos para encontrar los puntos de intersección de la recta con los ejes de plano cartesiano.