Ecuaciones Trigonométricas

Introducción

La palabra ecuación viene del latín, de aequatus, participio pasivo de aequare: "igual, volver igual". Una ecuación es una afirmación de igualdad entre dos expresiones matemáticas. Resolver la ecuación significa encontrar la o las condiciones requeridas o necesarias para que se cumpla la igualdad propuesta.

Así, cuándo se establece que:   

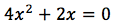
en ese momento se ha creado una ecuación, porque hay una afirmación de igualdad entre dos expresiones. Otra cosa distinta es investigar qué se requiere para que realmente:  

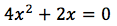
Cuando se hace esta investigación se llega a que "x" sea igual a cero (x=0), o bien que la x sea negativa y tenga el valor de un medio, estos valores son los que resuelven la ecuación.

Una ecuación no es una especie de "adivinanza numérica", es un planteamiento y un algoritmo para obtener el resultado. Por ejemplo: ¿qué número elevado al cuadrado es igual al doble de ese número más veinticuatro?".

El planteamiento es que se desconoce el número y lo representamos con una literal. Obteniendo la expresión: x(4x+2)=0  , para que el producto sea igual a cero es necesario que uno de los factores sea cero y se tiene que x= 0 o bien 4x+2=0.

Entonces, una ecuación trigonométrica también debe cumplir las condiciones antes mencionadas. Por ejemplo: "el seno de un ángulo más el coseno de ese mismo ángulo es igual a:  

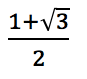
¿Cuál es ese ángulo? se puede comprobar con una calculadora que la respuesta es 30°; es evidente que esta respuesta no es posible encontrarla al tanteo. Debe existir un procedimiento de un planteamiento y desarrollo de algoritmos que lleve a la solución, este planteamiento es una ecuación trigonométrica.

Resolver la ecuación trigonométrica como la anterior es el objetivo primordial. Para su estudio y mejor compresión conviene clasificarlas de acuerdo al método de solución que le corresponda.

Despeje directo

Es la ecuación trigonométrica más sencilla, son las que se resuelven simplemente despejando la razón trigonométrica y posterior se aplica la función inversa para despejar el argumento de la razón. El argumento es el ángulo, que no necesariamente es "x", recuerde que el número de soluciones de una ecuación trigonométrica depende del intervalo de solución, considerando el número de vueltas en el círculo unitario. Generalmente se considera un intervalo de 0° a 360°, para este caso se tienen dos soluciones para las ecuaciones de primer grado y cuatro soluciones para las ecuaciones de segundo grado.

Ejemplo 1: 

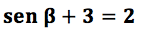
Al despejar el argumento primero se realiza operaciones contrarias de los términos. 

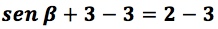
Al efectuar las restas correspondientes se obtiene: 

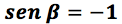
Se despeja el argumento:  

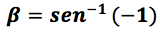
Se busca el valor de beta en el círculo unitario, en tablas o en calculadora, el resultado es 𝛃=270  

Ejemplo 2: 

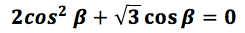
Para este tipo de expresiones antes de despejar hay que factorizar por factor común. Obteniéndose:  

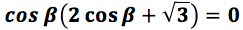
Para que se cumpla la igualdad uno de los factores debe ser cero. Por lo que se obtiene: 

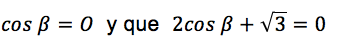
Al despejar de las dos expresiones, de la primera expresión se tiene que:   

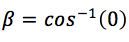
y de la segunda expresión:    

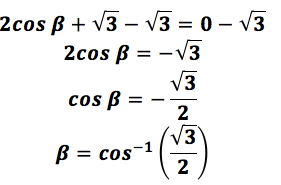
Cuando se tiene coseno inverso de cero, se obtiene un ángulo de 90° y para cuando se tiene coseno inverso de:    

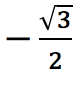
se obtiene los ángulos 150° y 210°. Por lo que las soluciones de esta ecuación son 90°, 150°, 210° y 270°. 

Ejemplo 3: 

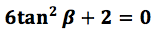
Al despejar utilizando las operaciones inversas se obtiene: 

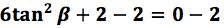
Al sumar términos semejantes se obtiene:    

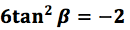
Se despeja utilizando las operaciones inversas se obtiene: 

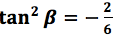
Simplificando la expresión se obtiene:  

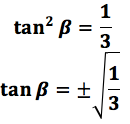
Por lo que las soluciones de esta ecuación cuadrática son: 

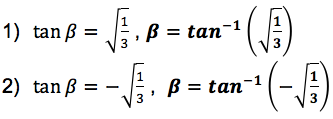
Por lo que las respuestas son: 30°, 150° 210° y 330°.

PASANDO TODOS A UNA SOLO RAZÓN TRIGONOMÉTRICA Y EMPLEADO FORMULA DE SEGUNDO GRADO.

Algunas ecuaciones trigonométricas pueden resolverse fácilmente cuando es posible pasarlas todas las razones trigonométricas que estén en la expresión a una sola razón, para ello se emplean las identidades básicas. En caso de que resulte una ecuación trigonométrica de segundo grado, se utiliza la formula general de las ecuaciones de segundo grado, teniendo en cuenta que la incógnita es la razón trigonométrica.

Es importante interpretar o entender el significado de una ecuación de segundo grado y de su fórmula general para resolverla. Por ejemplo, si se tiene la ecuación:   

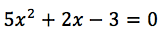
se interpreta de la siguiente manera: "cinco veces la incógnita al cuadrado, más dos veces la incógnita, menos tres es igual a cero". Esta expresión se puede resolver con la expresión: 

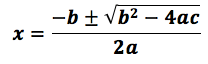
Lo esencial de este asunto está en entender, a que incógnita se le representa con la letra "x"; sin embargo, esa representación puede ser cambiada por cualquier otro símbolo. En caso de ser así, lo que se ha cambiado es nada más la representación, no la interpretación. Por ejemplo, se puede cambiar la representación de la incógnita, del caso anterior en vez de "x" se escribe  

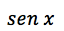
es decir, ahora representa la incógnita. De manera que "cinco veces la incógnita al cuadrado, más dos veces la incógnita, menos tres es igual a cero", se representa por:

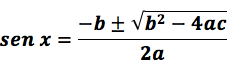
Un ejemplo de cómo se aplica este planteamiento es el siguiente.

Considerando la expresión: 

Para este caso solo hay que sustituir los valores numéricos en la expresión de la formula general. Es decir: 

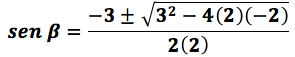
Al efectuar las operaciones: 

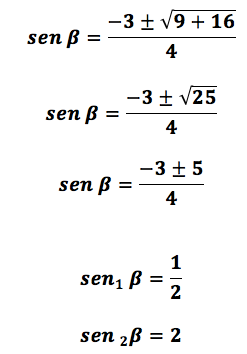
De los dos resultados el único que tiene solución es:  

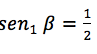
y los ángulos que cumplen con la ecuación son 30° y 150°.