Identidades Trigonométricas

Un número es el inverso de otro, respecto de cierta operación, si al operar ambos entre sí dan como resultado el elemento neutro de esa operación. Por ejemplo: en la suma el elemento neutro es el cero, ya que el cero no altera o deja inalterado a todo número. De manera que el inverso del número + 8 es el - 8, ya que al operar ambos dan como resultado el cero ( el elemento neutro de la suma). Por eso se le llama inverso aditivo. En la multiplicación, el elemento neutro es el uno, ya que el uno deja inalterado en la multiplicación a cualquier número. De manera que el inverso de 6 es 1/6, ya que en la multiplicación da como resultado el uno (elemento neutro de la multiplicación) por eso se le llama inverso multiplicativo. Un sinónimo de inverso multiplicativo es recíproco.

De tal manera que el significado que se le da a las seis razones trigonométricas es el de inverso multiplicativo, o sea que al multiplicarse entre sí dan el elemento neutro de la multiplicación el "1". Por otra parte, cabe recordar que si un número "n" es el inverso multiplicativo de otro número m, lo que significa que n*m = 1, entonces puede escribirse por simple despeje que n=(1/m) o bien m=(1/n).

Considerando las seis razones trigonométricas, se puede determinar que seno y cosecante son reciprocas o inversos multiplicativos, ya que de su multiplicación ((c.o.)/h)(h/(c.o.))=1; igualmente el coseno con la secante son inversos multiplicativos, ya que ((c.a.)/h)(h/(c.a.))=1 y de la misma forma la tangente con la cotangente también son inversos multiplicativos, si las multiplicamos se obtiene la unidad. De manera que las primeras tres expresiones se les denominan identidades trigonométricas inversas o reciprocas.

A las expresiones anteriores también se les conoce con el nombre de fórmulas de los recíprocos ya que, en particular, a los inversos multiplicativos se les llama recíprocos. Dos números son recíprocos si se invierten respectivamente el numerador con el denominador. Por ejemplo, 3/4 y 4/3 son recíprocos; 2/9 y 9/2 so recíprocos. Es claro que si se multiplican entre si dan la unidad, o sea el elemento neutro de la multiplicación. Los recíprocos son también inversos.

Al considerar las cuatro primeras razones trigonométricas que son: seno, coseno, tangente y cotangente con la operación división, de obtiene lo siguiente.

Dividiendo el seno entre el coseno se tiene ((sen x)/(cos x))= tan x y dividiendo el coseno entre el seno se tiene(cos x)/(sen x))= cot x. Estas dos expresiones se le denominan identidades trigonométricas de cociente o división.

Al elevar al cuadrado las razones trigonométricas seno y coseno, que al sumarlas se obtiene la expresión:

que se denomina identidad pitagórica. Significa que para cualquier ángulo, la suma del seno al cuadrado de ese ángulo más el coseno al cuadrado del mismo ángulo siempre se va obtener la unidad.

Dividiendo la expresión anterior entre la razón seno al cuadrado, por otra parte usando las identidades trigonométricas recíprocas y elevándolas al cuadrado, para realizar las operaciones correspondientes. Todo esto se representa en las siguientes expresiones.

Al repetir el procedimiento, pero con la división de coseno al cuadrado, se obtiene la expresión:

Las expresiones:

Se les conoce como identidades trigonométricas pitagóricas. Las identidades reciprocas, cociente y Pitagóricas, se le da el nombre de identidades básicas. Al realizar despejes de dichas expresiones, se obtienen otras que representan una equivalencia de las ocho identidades básicas.

DEMOSTRACIONES DE LAS IDENTIDADES TRIGONOMÉTRICAS

Dada una expresión trigonométrica, para demostrarla consiste en transformarla hasta convertirla en una igualdad que sea cierta sin lugar a dudas.

Las demostraciones trigonométricas se hacen de tal manera que no utilicen nada dudoso, ni nada falso, para que la conclusión no sea dudosa o falsa. Todo debe ser cierto sin dar lugar a dudas para que la demostración sea válida. ¿Y qué es cierto sin lugar a dudas?: Por una parte, las ocho expresiones básicas de las identidades trigonométricas lo son, por eso se dedujeron paso a paso para verificar su validez y veracidad, por otra parte, toda identidad es cierta sin lugar a dudas por ser axiomática. Una identidad es cualquier cosa igual a sí misma. Axiomático es aquello tan evidente que no requiere demostración.

Para demostrar una proposición trigonométrica debe transformarse, ya sea por sustituciones de cualquier de los términos o factores algebraicos válidos, de manera que se llegue a una igualdad que sin duda alguna sea cierta, es decir, que lo escrito del lado izquierdo sea realmente igual a lo escrito del lado derecho de la igualdad.

Ejemplo:

Demuestra la siguiente identidad.

Para demostrar la identidad trigonométrica se tiene que considerar las siguientes sugerencias y como tal no tienen un orden de aplicación y se pueden repetir tantas veces que sea necesario.

Sugerencias para demostrar identidades

Se debe iniciar de la parte más compleja de la expresión para transformarse en el lado más sencillo de la igualdad.
Sustituir la razón tangente, cotangente, secante y cosecante en función de senos y cosenos.
Realizar las operaciones algebraicas que se indican.
Utilizar las identidades básicas, adaptándolas a nuestras necesidades.
Tener presente el objetivo, al que se pretende llegar. Que es la otra parte de la igualdad.

Para dicho ejemplo se considera la parte izquierda de la expresión y se debe llegar a la parte derecha

Se inicia considerando las identidades trigonométricas básicas, de las ocho se selecciona dos que son:

y para adaptarlas a las necesidades del ejercicio por lo que se despejan la segunda expresión quedando:

Al sustituir las respectivas equivalencias en la parte izquierda se obtiene la siguiente expresión:

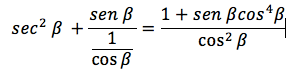
Al realizar la operación de simplificación de la fracción compleja se obtiene.

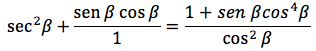
Al utilizar la identidad básica se despeja y toda la expresión obtenida se eleva al cuadrado

Que al sustituirla en la expresión que se demuestra se obtiene.

Al sumar las fracciones correspondientes se obtiene:

Al realizar la multiplicación de los factores comunes y aplicando leyes de exponentes se obtiene:

Por lo que se concluye la demostración.