Funciones Trigonométricas

Las funciones las comprendemos como la relación de dos objetos distintos los cuales presentan una relación. Ejemplos se tiene muchos, uno de ellos es el costo de producción y el número de piezas producidas, se tiene claro que a mayor número de piezas menor es el costo por unidad. Otro es la contaminación de una ciudad depende de la cantidad de vehículos circulando, uno más podría ser la presión depende la temperatura.

En todos estos ejemplos se nota la dependencia de un conjunto con respecto a otro y su regla de correspondencia entre dichos conjuntos.

La definición la comprendemos como: "Una función f de un conjunto A a un conjunto B es una regla que se asigna a cada elemento de A exactamente un elemento del conjunto B".

Todos los elementos del conjunto A se denomina Dominio de la función y todos los elementos del conjunto B se denomina rango de la función.

Aun cuando el dominio de la función puede ser cualquier colección de personas, objetos, ciudades, etc. aquí solo consideramos el conjunto de los números ℝ y lo representamos por la variable "x", llamada variable independiente.

Al rango es el conjunto B lo representamos por la variable "y", sus valores depende de los valores de la variable dependiente.

Las funciones trigonométricas son muy utilizadas en la ciencias naturales para analizar fenómenos periódicos tales como: movimiento ondulatorio, corriente eléctrica alterna, cuerdas vibrantes, oscilaciones de péndulos, ciclos comerciales, movimientos periódicos de los planetas, ciclos biológicos, etc. en la aplicación de las funciones trigonométricas relacionadas con fenómenos que se repiten periódicamente, se requiere que su dominio sea el conjunto de los números reales. Para la obtención de los valores de las funciones trigonométricas de números reales es mediante el uso de calculadora o tablas trigonométricas, si el ángulo es notable podemos emplear el cuadrado o el triángulo equilátero.

FUNCIÓN SENO

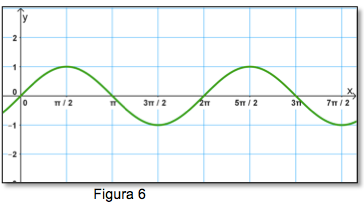
La función seno está definida por: f(x) = sen x

Las características de la función seno son:

Dominio: R
Recorrido: [-1, 1].
El período de la función seno es 2pi.
La función y = sen x es impar, ya que sen(- x ) = - sen x, para todo x en R.
La grafica de y= sen x intercepta al eje X en los puntos cuya abscisas son: x= np para todo número entero n.
El valor máximo de sen x es 1, y el mínimo valor es -1.
La amplitud de esta función es 1.

La gráfica en posición normal de la función seno es:

FUNCIÓN COSENO

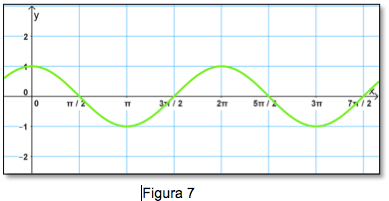
La función coseno está definida por: f(x) = cos x.

Las características de la función coseno son:

· Dominio: R

· Recorrido: [-1, 1]

· Es una función periódica, cuyo periodo es 2pi.

· La función y = cos x es par, ya que cos (-x) = cos x, para todo x en R

· La grafica de y = cos x, intercepta al eje X en los puntos cuyas abscisas son: para todo número entero n.

· El valor máximo de cos x es 1, y el valor mínimo es -1.

· La amplitud de la función y = cos x es 1.

La gráfica en posición normal de la función coseno es:

FUNCIÓN TANGENTE

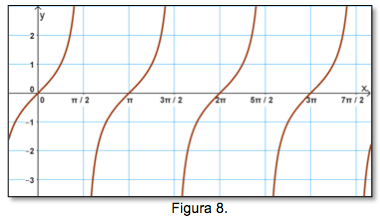
La función tangente está definida por: f(x) = tan x.

Las características de la función tangente son:

Dominio: R-⟦(pi/2)+pi*n⟧
Recorrido: R
La función tangente es una función periódica, cuyo periodo es pi .
La función y = tan x, es una función impar, ya que tan (-x) = -tan (x)
La gráfica de y = tan x intercepta al eje X en los puntos cuyas abscisas son: x=n*pi, para todo número entero n.
El valor máximo de tan x es infinto , y el valor mínimo es menos infinito.
La amplitud de la función y = tan x es .

La gráfica en la posición normal de la función tangente es:

Las otras funciones trigonométricas que son: cotangente, secante y cosecante también son funciones periódicas. Cuyas gráficas se muestran a continuación.

La gráfica en la posición normal de la función cotangente es:

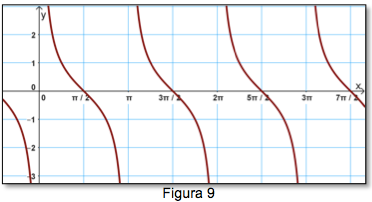
La gráfica en la posición normal de la función secante es:

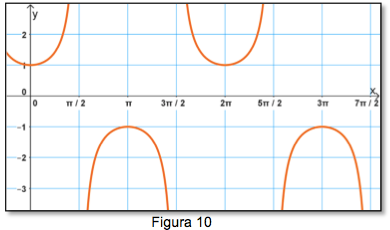
La gráfica en posición normal de la función cosecante es:

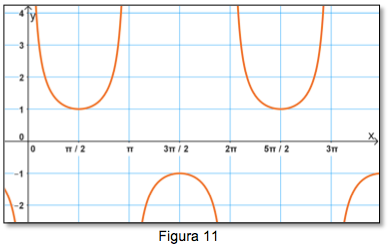
TRANSFORMACIÓN DE LAS GRÁFICAS DE LAS FUNCIONES TRIGONOMÉTRICAS.

La forma para desplazar, ampliar, contraer, reflejar la gráfica de una función trigonométrica se puede realizar mediante la suma, multiplicación, división de un número a toda la función o al argumento de la función. Como lo muestra la siguiente expresión:

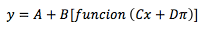
Donde A representa el desplazamiento vertical, dependiendo del signo de A es hacia arriba o hacia abajo. Considerando la posición normal de la gráfica y el módulo de A.

B representa la ampliación o reducción en forma vertical de la gráfica, cuando B tiene un valor entero es ampliación, si B es una fracción menor que la unidad es una reducción de la respectiva gráfica (tangente, cotangente, secante y cosecante no presentan ampliación reducción).

C representa la ampliación o reducción en forma horizontal de la gráfica, cunado C es entero la gráfica presenta una reducción, si B es una fracción es una ampliación de la respectiva gráfica.

D representa el desplazamiento horizontal de la respectiva gráfica.

CARACTERÍSTICAS DE ESTA FUNCIONES

La gráfica de las funciones representadas por las expresiones:

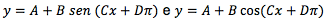
considerando que C>0, se puede obtener a partir de la gráfica de las funciones y=sen x e y = cos x, cuyas características se señalan a continuación

Amplitud: IBI, que es el promedio de la diferencia entre los valores máximo y mínimos de la función.
Periodo:para la función normal es : 2pi , para la función con desplazamiento horizontal es (2pi/C)
Desfase: (-D/C), desplazamiento horizontal de (-D/C) a la derecha o al izquierda si D es un valor negativo.
· Desplazamiento vertical: traslación vertical en A unidades de la gráfica normal, si A es positivo es hacia arriba y cuando A es negativo hacia abajo.
Un ejemplo se muestra en la figura 12, que está representada por la expresión:

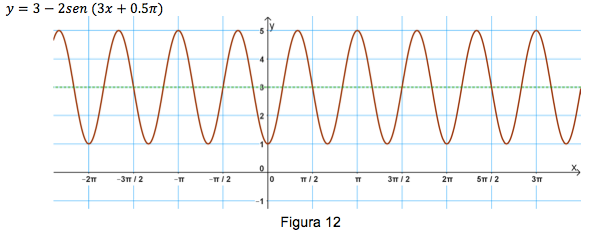
De la figura 12, se puede observar que la gráfica se ha desplazado 3 unidades hacia arriba, como el coeficiente de sen es 2 y negativo, la gráfica inicia 2 unidades en la parte abajo considerando centro de la gráfica. Su desfase es hacia la parte izquierda con un valor de (0.5*Pi/3).