Ángulos Cuadrantales y Coterminales
Considerando un ángulo con vértice en el origen del plano cartesiano y su posibilidad de ser positivo o negativo, da origen a una nueva clasificación de los ángulos en plano cartesiano que son:
Ángulos en posición normal: es aquel ángulo que su vértice está en el origen, su lado inicial coincide con el eje positivo de las X y su otro lado del ángulo se encuentra en cualquier cuadrante.
Ángulos Coterminales: son aquellos ángulos que se encuentran en posición normal y sus lados terminales es el mismo solo que un ángulo es positivo y el otro ángulo es negativo, o bien que ambos son positivos o negativos pero uno es mayor que otro en múltiplos de 360°. Así que lo importante de estos ángulos es que sus lados terminales sean los mismos, esto implica que para un solo ángulo exista una afinidad de ángulos coterminales.
Ángulos cuadrantales: son aquellos ángulos en posición normal, cuyo lado final coincida con cualquier semieje del plano cartesiano. La medida de estos ángulos siempre serán múltiplos de 90°
Ángulos reducidos: un ángulo en posición normal que se encuentra situado en el segundo, tercero o cuarto cuadrante, siempre es posible relacionarlo con otro del primer cuadrante, cuyas razones trigonométricas tenga los mimos valores.
La relación entre las razones trigonométricas de los ángulos situados en los distintos cuadrantes con el primer cuadrante, resulta esencial porque existen tablas solo para el primer cuadrante.
Si se desea calcular el valor de las razones trigonométricas para cualquier valor de un ángulo, lo que se hace es asociarle un triángulo rectángulo a cada ángulo, este triángulo rectángulo se construye trazando un segmento paralelo al eje de las ordenadas (Y), desde el punto de intersección entre el lado del ángulo y la circunferencia, hasta el eje de las abscisas (X), como lo muestra la figura 4.
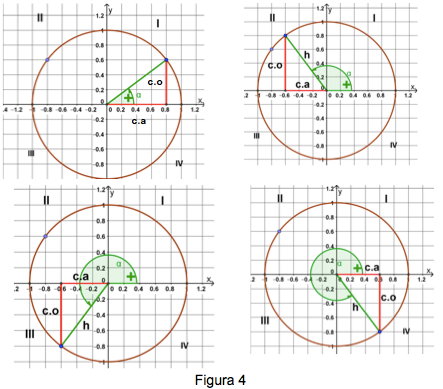
Al observar la figura 4, se dará cuenta que los catetos opuesto y adyacentes cambia de signo de acuerdo al cuadrante en que se encuentren y la hipotenusa es siempre positiva. Esto implica que las razones trigonométricas en el plano cartesiano tienen asociado el signo negativo o positivo, dependiendo del cuadrante donde se encuentre el triángulo rectángulo y de la definición de la razón trigonométrica.
Como los ángulos también pueden ser negativos, implica que también se pueden obtener razones trigonométricas para ángulos negativos es decir: sen(-𝜷) ,cos(-𝜷) . Esto es para cada una de las definiciones de las razones trigonométricas.
Además los ángulos pueden ser mayores a 360° o 2pi, esto significa que los ángulos pueden dar una vuelta o varia vueltas.
