Distancia entre dos puntos
DISTANCIA ENTRE DOS PUNTOS
Una vez localizados dos puntos cualesquiera en el plano cartesiano, el siguiente procedimiento es encontrar la distancia entre dichos puntos, si los puntos son representados por los pares ordenados
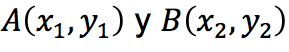
con la condición de que al unirlos no formen rectas verticales u horizontales y se pueda trazar un triángulo rectángulo, donde el segmento AB sea la hipotenusa de dicho triángulo. Como se muestra en la figura 2
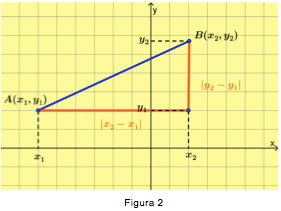
Las longitudes de los catetos de la figura 2, están determinados por las expresiones
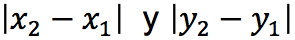
la distancia entre los puntos A y B es la longitud de la hipotenusa del triángulo. Empleando el teorema de Pitágoras que dice "En todo triangulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos", por lo que se obtiene lo siguiente:
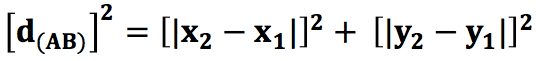
Al realizar las respectivas operaciones se obtiene:
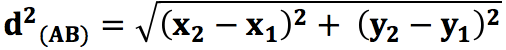
Al considerar que los puntos A y B están en la misma vertical o en la misma horizontal, uno de los dos sumados de la expresión anterior es cero, pero el resultado sigue siendo verdadero.
De la expresión anterior, además de permitir la distancia entre dos puntos, nos permite solucionar los siguientes problemas:
- Determinar el perímetro de un triángulo rectángulo o de algunas otras figuras geométricas.
- Comprobar que el triángulo mostrado es un triángulo rectángulo, aplicando el teorema de Pitágoras a las distancias obtenidas y al verificar que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
- Comprobar que la figura mostrada es un triángulo isósceles, cuando las distancias obtenidas son iguales.
- Comprobar que es un triángulo equilátero, si sus tres lados son iguales.
