Notas

Lo mismo que las medidas de longitud, superficie, tiempo, volumen, etc. son magnitudes que se pueden medir en metros, metros cuadrados, segundos, litros, etc. los ángulos también son magnitudes que pueden medirse, de mayor o menor apertura; los lados de un ángulo deben tener unidades de medición, para determinar qué tan grande o pequeña es la magnitud.

La distancia se puede medir utilizando diversa unidades o sistemas de medidas de longitud. Por ejemplo, una distancia puede medirse en metros, en kilómetros, en centímetros, en millas, etc. (múltiplos y submúltiplos). No obstante si conocemos una distancia en una de estas unidades es posible pasarla a otra, por ejemplo si se conoce una distancia en kilómetros se puede conocer en centímetros. Algo similar ocurre con los ángulos. Existen diversas unidades para medir los ángulos, siendo las más usuales las siguientes.

El radian. Un radian es el ángulo central de un circulo que le corresponde un arco de circunferencia cuya magnitud es igual al radio de dicha circunferencia. Como lo muestra la figura 1.13

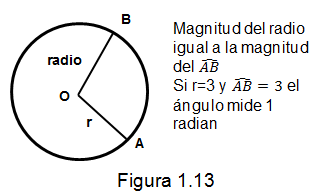
Si consideramos un arco de circunferencia cuya longitud fuese el doble del radio, el ángulo central correspondería a una medida de dos radianes.

Considerando un ángulo completo le corresponde un arco igual a la circunferencia, es decir un a vuelta completa, cuya longitud del arco es igual a 2pi.

Grados sexagesimales. Es otra unidad básica para medir los ángulos, se define a partir de un ángulo completo, es decir a una circunferencia la cual se divide en 360 partes, a cada una parte se le denomina grado sexagesimal. El símbolo que se emplea para expresar los grados sexagesimales es °, expresado en forma de potencia en el número que indica la medida del ángulo que se indique.

Considerando un ángulo completo, que sus medidas son 2pi radianes y 360°, se obtiene la siguiente equivalencia 2pi rad = 360°, que al simplificar es pi rad = 180°

Submúltiplos del grado sexagesimal. Lo mismo que un kilómetro se divide en 1000 partes y cada una de ellas en 100 centímetros y un centímetro lo dividimos en 10 partes, esta porción representa un milímetro del metro. El grado sexagesimal también puede dividirse en parte equivalentes y cada una de esas partes es un submúltiplo, así tenemos:

Minuto. A un grado sexagesimal lo dividimos en sesenta partes iguales, a cada una de esas partes se le denomina minuto. Por lo que se deduce que un grado tiene sesenta minutos. A los minutos los representamos con el símbolo " ´ ", expresado en forma de potencia en el número que indica la medida del ángulo que se trabaja. Al representarlo en forma de equivalencia se tiene 1° = 60´, de la misma forma a un minuto lo dividimos en sesenta partes iguales, a cada parte de le denomina segundo que se representa por el símbolo ", expresado en forma de potencia en el número que indica la medida del ángulo que se trabaja. Por lo que se deduce que un minuto es igual a sesenta segundo es decir 1´ = 60"

De esta forma se obtiene que un ángulo se puede expresar con mayor exactitud en su medida, como el siguiente ejemplo b= 31° 17´ 23"

Grado centesimal. Es otra unidad básica para medir los ángulos, se define partir de un ángulo completo, es decir de una circunferencia la cual se divide en 400 partes equivalentes, a cada una de esta partes de le denomina grado centesimal. El símbolo que se emplea para expresar los grados centesimales es g, expresado en forma de potencia en el número que indica la medida del ángulo. A cada grado centesimal de divide en 100 partes equivalentes, a cada una de estas partes se les denomina minutos, que se representan por el símbolo m, expresado en forma de potencia en el número que indica la medida del ángulo. A cada minuto se divide en 100 partes equivalentes, a cada una de estas partes se les denomina segundos, que se representan por el símbolo s, expresado en forma de potencia en el número que indica la medida del ángulo.

De esta forma se obtiene que un ángulo puede expresar como b =20g 30m 17s

TIPOS DE ÁNGULOS

Ángulos por su posición con otro ángulo. Se clasifican de acurdo a su posición con otro ángulo que puede ser adyacentes, consecutivos y opuestos por el vértice.

Ángulos adyacentes. Son aquellos que tienen un vértice y un lado común, como lo muestra la figura1.14    

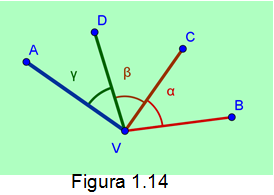
Ángulos consecutivos. Son los que presentan un lado en común, con vértice distinto. Como lo muestra la figura 1.15

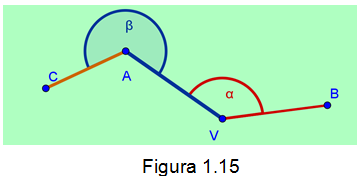
Los ángulos 𝛼 y 𝛽 son consecutivos porque comparten el mismo lado pero no tienen vértice común.

Ángulos opuestos por el vértice. Son pares de ángulos, cuyos lados forman pares de segmentos opuestos, como lo muestra la figura1.16

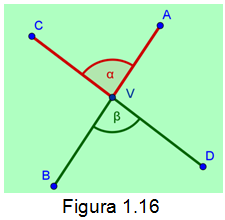
Además los ángulos 𝛼 y 𝛽 de la figura 1.16 son congruentes, es decir presentan la misma magnitud en su tamaño.

Pareas de ángulos que la suma de sus medidas siempre es un valor constante

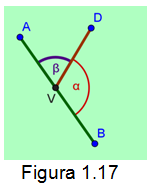
Ángulos suplementarios. Son dos ángulos adyacentes cuya suma de sus medidas es de 180° o pi rad. Como lo muestra la figura 1.17

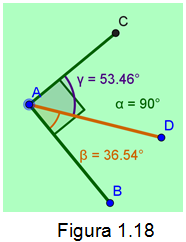
Ángulos complementarios. Son dos ángulos adyacentes cuya suma de sus medidas es de 90° o pi/2 rad. Como lo muestra la figura 1.18

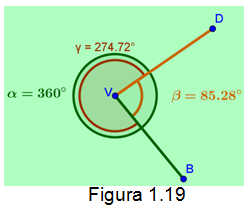
Ángulos conjugados. Son dos ángulos adyacentes cuya suma de sus medidas es de 360° o 2pi rad. Como lo muestra la figura 1.19

Ángulos por su posición entre rectas paralelas e interceptadas por una secante

Al ser interceptadas rectas paralelas por una secante se forman distintos tipos de ángulos, que son los siguientes.

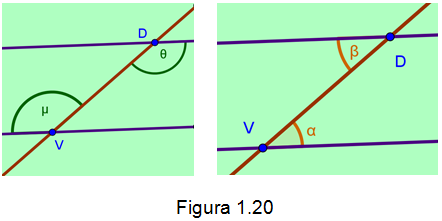
Ángulos alternos internos. Son dos ángulos que se encuentran situados dentro de las paralelas, uno de estos ángulos está ubicado del lado derecho de la secante y el otro del lado izquierdo, además dichos pares de ángulos son congruentes. Como lo muestra la figura 1.20.

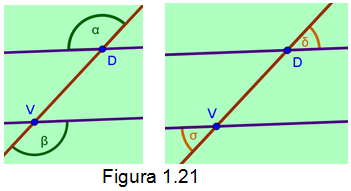
Ángulos alternos externos. Son dos ángulos que se encuentran situados fuera de las rectas paralelas, uno de estos ángulos está ubicado del lado derecho de la secante y el otro del lado izquierdo, además dichos ángulos son congruentes. Como lo muestra la figura 1.21 

Ángulos correspondientes. Son aquellos pares de ángulos que quedan en el mismo lado de la recta secante y además no son adyacentes. Pueden ser un externo con un interno. Además dichos ángulos son congruentes, como lo muestra la figura 1.22 

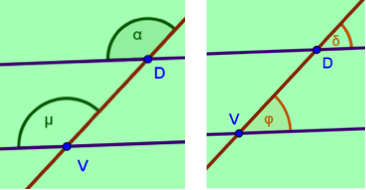
Figura 1.22

Ángulos colaterales. Son dos ángulos un agudo y un obtuso que están situados en el lado derecho o del lado izquierdo de la secante y además son adyacentes.

Actividad