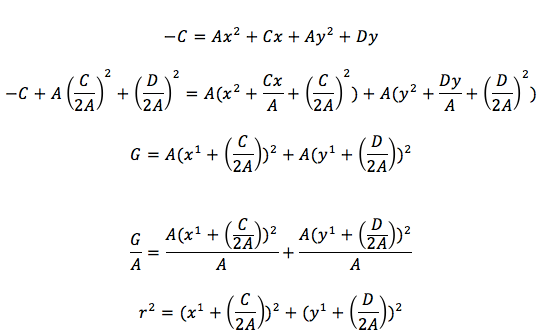Circunferencia

Definición: es el lugar geométrico formado por el conjunto de puntos P(x,y) que se encuentra a la misma distancia (equidistantes) de un punto fijo denominado centro.

De acuerdo a la definición localizamos el punto O (h,k) en el plano cartesiano y se encuentra todos los puntos P (x,y) que están a la misma distancia. Como lo muestra la figura 1.1

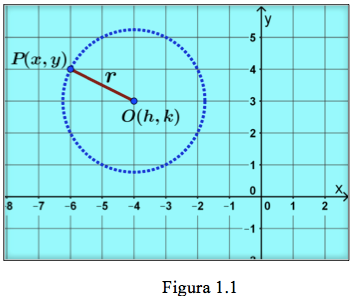
Considerando los puntos P (x,y) y O (h, k) de la figura 1.1 y aplicando la expresión de distancia entre dos puntos:  

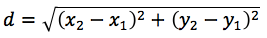
y para la figura 1.1 se obtiene 

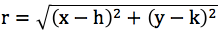
elevando al cuadra para eliminar la raíz, se obtiene:   

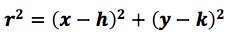
Esta última expresión es la forma ordinaria de la circunferencia, esta representación  nos permite obtener en forma directa el radio y el centro de la circunferencia, que se encuentra determinado por r = radio y el centro (h,k),  que son los elementos suficientes para trazar la gráfica de la circunferencia.

Si el centro de la circunferencia coincide con el centro del plano cartesiano las coordenada del centro son (0,0) y la expresión de la circunferencia adquiere la forma

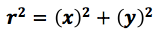
Cuyo nombre es ecuación canónica de la circunferencia.  

 Al considerar la expresión:  

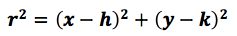
y desarrollarlos binomios se obtiene la expresión:  

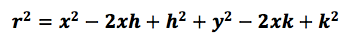
Que al sumar y multiplicar las literales que representan valores constantes, se obtiene la siguiente representación:  

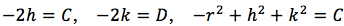
que al sustituirlas en la expresión anterior adquiere la forma: 

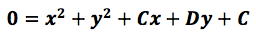
Esta última expresión se denomina ecuación general de la circunferencia, además para este caso los coeficientes de los términos cuadráticos es uno, existen otros caso en que los coeficientes son diferentes de uno pero iguales en los cuadráticos. Por lo que la ecuación adquiere la forma:  

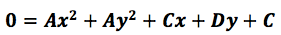
Cuando se tiene la ecuación general de la circunferencia y se requiere conocer el radio y el centro de ésta, se tiene que transformar la ecuación la forma ordinaria, con el siguiente procedimiento. El primer paso es ordenar las variables, el segundo es realizar un factor común considerando los coeficientes de los términos cuadráticos para cada variable, el tercer paso es completar trinomios cuadrados perfectos para cada variable, el cuarto paso factorizar los trinomios cuadras perfectos y por último dividir. Que al realizar cada uno de estos pasos de obtiene lo siguiente: