POLÍGONOS

Un polígono es una figura geométrica limitada por segmentos de rectas denominados lados, donde el extremo de un segmento es el origen del otro segmento y se llegan a unir de tal forma que se cierra la figura por los segmentos.

Etimológicamente, la palabra POLÍGONO proviene de las raíces poli que significa muchos y gonos que significa ángulos. Por lo que su significado de polígono es una figura de muchos ángulos, como el número de los ángulos es igual al número de lados, la palabra polígono se define como figura cerrada de muchos lados.

Ejemplos de polígonos

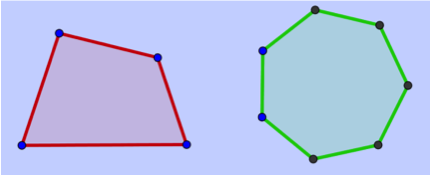
Figura 1

Los polígonos se nombran mediante letras mayúsculas situadas en los vértices del mismo. Su notación se efectúa escribiendo las letras mayúsculas después de la palabra polígono o del nombre especifico del polígono, por ejemplo el triángulo ABC, pentágono ABCDE, también por sus símbolos gráficos.

Las partes fundamentales de los polígonos son los siguientes.

Lados: son los segmentos de rectas que forman al polígono o delimitan a este con el resto del plano.

Vértices: es el nombre que reciben los puntos de intersección de los lados del polígono. Dichos puntos nos permiten dar el nombre específico del polígono.

Ángulos interiores: son aquellos formados por dos lados del polígono y su región angular queda en la región interna de este.

Ángulos exteriores: región angular formada a partir de un lado del polígono y la prolongación del lado adyacente a él.

Perímetro: es la suma de las medidas de los segmentos de un polígono, también recibe el nombre de contorno.

Diagonales: son los segmentos que están delimitados por dos vértices no consecutivos.

Radio de un polígono regular: es el segmento determinados por el punto denominado centro del polígono y uno de sus vértices.

Ángulo central: es la región formada por dos radios consecutivos del polígono, la suma de todos los ángulos centrales de un polígono es de 360°

Apotema de un polígono regular: es el segmento delimitado por el punto denominado centro del polígono y el punto medio de un lado, además dicho segmentos es perpendicular al lado.

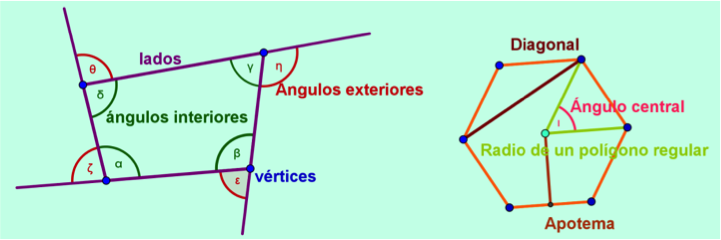
Figura 2

CLASIFICACIÓN DE POLÍGONOS

Se han determinado tres clasificaciones para los polígonos que son las siguientes:

• Por la amplitud de sus ángulos.
• Por la medida de sus lados y sus ángulos
• Por el número de sus lados

Por la amplitud de sus ángulos

Convexo: son aquellos polígono que sus ángulos interiores son todos menores de 180° y al trazarles una recta secante sólo pueden ser intersectados en dos puntos. Ver figura 3.

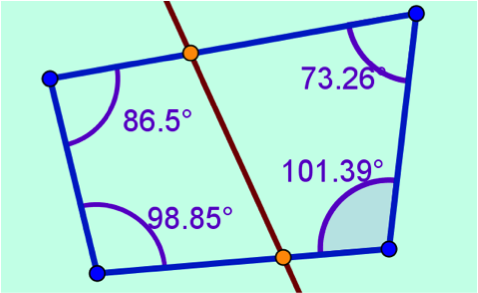
Figura 3

Cóncavos: son aquellos polígonos que uno o más de sus ángulos son mayores a 180° y al trazarles una secante pueden ser cortados en más de dos puntos. Ver figura 4

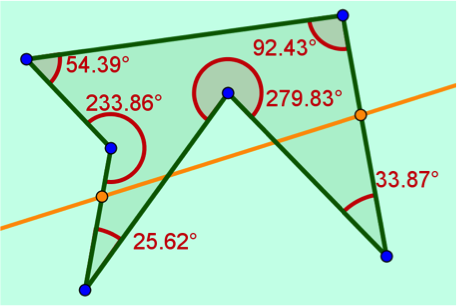
Figura 4

Por la medida de sus lados y ángulos

Regulares o equiángulos: son aquellos polígonos que sus lados y ángulos son iguales entre sí. Ver figura 5 

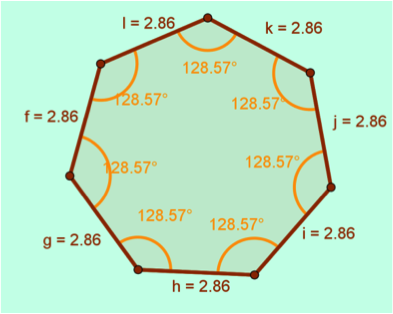
Figura 5

Irregulares: son aquellos polígonos que uno o más de sus lados o ángulos son diferentes a los demás. Ver figura 6.

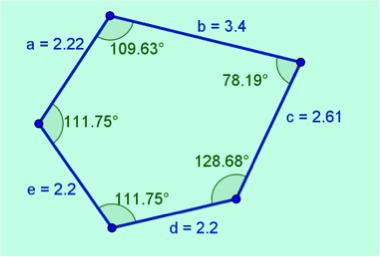
Figura 6

Por el número de lados

En esta clasificación los polígonos reciben nombres específicos de acuerdo al número de lados que presentan, y lo nombres cumplen determinados lineamientos como lo muestra la tabla de la figura 7.

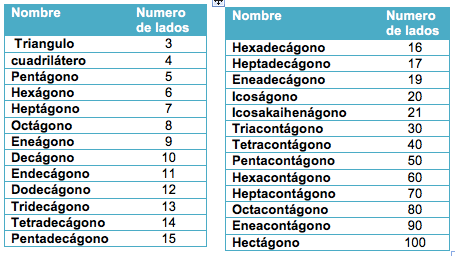
Figura 7

 TEOREMAS SOBRE POLÍGONOS

Teorema 1: la suma de los ángulos interiores de cualquier polígono es igual al producto de dos ángulos rectos por el número de lados del polígono restándole dos.

La medida de cada ángulo interior de un polígono regular de n lados, se puede calcular por medio de la siguiente expresión.

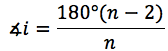
Teorema 2: La suma de los ángulos exteriores de cualquier polígono es igual a 360°

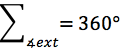
La medida de cada ángulo exterior de un polígono regular de n lados se puede calcular por medio de la siguiente expresión.

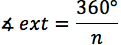
Teorema 3: EL número de diagonales totales de cualquier polígono de n lados es igual al mitad del producto de n por n menos 3.

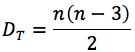
El número de diagonales que puede trazar desde un vértice de cualquier polígono de n lados es igual al número de lados restando 3.

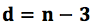
Teorema 4: En un paralelogramo, los dos lados opuestos son iguales y los dos ángulos opuestos a los lados son iguales.

Teorema 5: En un paralelogramo las diagonales se bisecan, es decir se intersectan en su puntos medios respectivamente.