Puntos, rectas, planos y ángulos

Notas

Punto

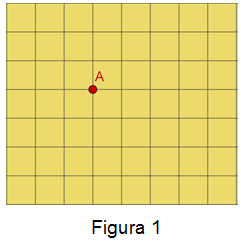
Es seguro que encuentres la idea de punto en diferentes contextos y para cada uno tenga un significado especifico, es este caso nos referimos al geométrico. Lo definimos como la figura o lugar geométrico que no tiene dimensiones y describe la posición en el plano o espacio. Se representa por una letra mayúscula, como lo muestra la figura 1.1

PLANO

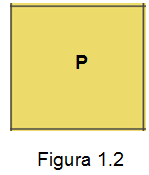
Consideremos "p" como un plano. Recuerde que un plano es una figura infinita, abstracta y no tangible (no tiene grosor). En general asociamos la idea de plano o parte de un plano a una superficie lisa, como ejemplos tenemos el folder, una hoja de la libreta, el pizarrón, una pared del salón de clases, etc. Como se muestra en la figura 1.2

RECTA

La línea está considerada como un sucesión de puntos en forma indefinida o como la huella continua que deje un la lápiz o lapiceros al moverlo en una hoja.

Existen diferentes tipos de líneas, que las denominamos según su forma, estas son: líneas rectas si la sucesión de puntos no cambias de dirección por ejemplo un haz luminoso, líneas curvas si la sucesión de puntos cambian de dirección por ejemplo las líneas formadas por el campo magnético de la tierra, líneas aduladas si la sucesión de puntos forman curvas del mismo tamaño y esta se repiten por ejemplo las líneas que describen las olas, las líneas mixtas que son la combinación de cualquiera de esta líneas. Una semirrecta es una porción de una recta que tiene un origen pero no tiene fin. Un segmento es una porción de una recta que tiene origen y fin.

Sean L y S dos semirrectas que comparten como origen el mismo punto O. El plano quedará dividido en dos regiones o partes de forma infinita, cada una de esas partes del plano definen a un ángulo, de donde se concluye, que dos semirrectas con el mismo origen forman dos ángulos. Como lo muestra la figura 1.3

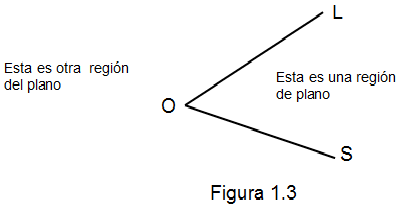
La figura 1.3 ilustra el concepto de ángulo. Observe que el plano en este caso es la hoja y ha quedado dividido en dos regiones infinitas. Una de ellas está formada por una región o espacio más pequeño y la otra por un espacio más grande. Observe que cada una de las regiones siempre una va a ser menor que la otra lo que implica que siempre se formaran dos ángulos uno mayor y otro menor.

Pongámosle nombre a cada uno de los elementos que interviene en un ángulo (figura 1.3)

O es un punto del plano se llama Vértice del ángulo.

L, S son semirrectas de origen O y se llaman lados del ángulo.

FORMAS DE EXPRESAR UN ÁNGULO

Existen diversas maneras de expresar un ángulo. Se mencionaran las más usadas en el tema de geometría

• Con letras griegas minúsculas 𝛼, 𝜷, etc. 
• Utilizando el nombre del vértice con letras mayúsculas y con un en la parte superior. 
• Empleando el nombre el vértice y un punto de cada lado de los segmentos que forman el ángulo. Ejemplos LOS, ABC, RTS. Observe que el nombre del vértice siempre está en el centro de las letras y además describe como estoy observando el ángulo.

Como siempre se forma dos ángulos, para indicar cuál de los dos de ellos nos referimos es común señalarlo con un línea curva entre los dos lados. Como lo muestra la figura 1.4

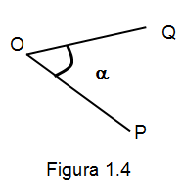
En la figura 1.4 se muestra el ángulo al que nos referimos y se puede nombrar  como: ángulo 𝛼 o bien como ángulo alpha o también ángulo POQ

ÁNGULO ORIENTADO, SENTIDO Y SIGNO DE UN ÁNGULO

Es conveniente dar a los ángulos una orientación o sentido, de las dos posibilidades que puede tener un ángulo, a cada una de estas posibilidades se le asigna un signo positivo o negativo. Considerando la figura 1.4, el ángulo 𝛼 tiene por vértice "O" y sus lados son "OP" y "OQ", considerar el 𝛼 y el sentido del lado "OP" hacia el lado "OQ" o bien el lado "OQ" hacia el lado "OP", como lo muestra la figura 1.5.

En la figura 1.5 se ha orientado el ángulo, mediante una flecha que indica el sentido. El ángulo de la izquierda se puede observar que el sentido es el  movimiento contrario a las agujas de un reloj y se le asigna el signo positivo. El ángulo de la derecha su sentido es el mismo que el movimiento de las agujas de un reloj y se le asigna el signo negativo.

Un ángulo está orientado cuando se le asigna un signo positivo o negativo, en algunas aplicaciones solo se considera la medida o magnitud del ángulo y no tiene relevancia el signo, existen situaciones donde es importante la magnitud del ángulo y su orientación o sentido.

ÁNGULOS OPUESTOS.

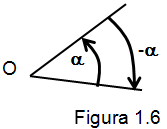
Si 𝛼 es un ángulo orientado se le ha asignado un signo positivo o negativo, al ángulo que presente los mismos lados y es de igual tamaño pero con signo contrario se le denomina ángulo opuesto a 𝛼 y se representa por -𝛼 y viceversa. Como lo muestra la figura 1.6

CASOS PARTICULARES DE ÁNGULOS

Se mencionarán algunos ángulos que son especiales por su magnitud o medida.

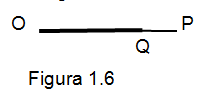
Ángulo nulo. Los dos lados del ángulo forman un único segmento y la apertura entre dichos lados es cero. Como lo muestra la figura 1.7 

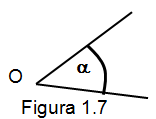
Ángulo agudo. Son dos segmentos de recta que forman al ángulo, solo se considera la región en el plano que tiene una magnitud mayor a cero grados y menor a noventa grados. Como lo muestra la figura 1.7

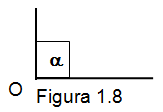
Ángulo recto. Los dos segmentos que forman al ángulo son perpendiculares y forman una región en el plano que tiene una magnitud de noventa grados. Como lo muestra la figura1.8   

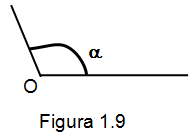
Ángulo obtuso. Los dos segmentos que forman al ángulo, forman una región en el plano que tiene una magnitud de más de noventa grado y menor de ciento ochenta grados. Como lo muestra la figura 1.9

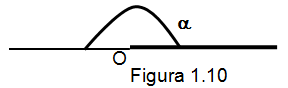
Ángulo llano o colineal  Los dos segmentos que forman al ángulo, forman una región en el plano que tiene una magnitud de ciento ochenta grados. Como lo muestra la figura 1.10. 

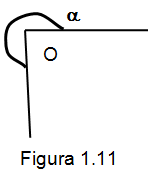
Ángulo cóncavo. Los dos segmentos que forman al ángulo, forman una región en el plano que tiene una magnitud de más de ciento ochenta grados y menor a trescientos sesenta grados. Como lo muestra la figura 1.11.

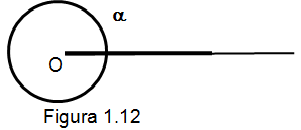
Ángulo completo o perígono. Los dos segmentos que forman al ángulo, forman un único segmento y la región que forman es un círculo. Como lo muestra la figura 1.12   

Actividad